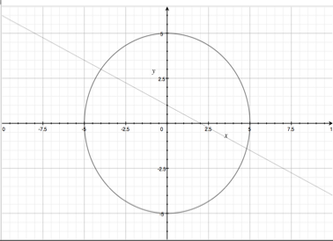
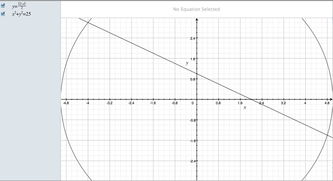
1) If you have a line equation 𝑥+2𝑦=2 and circle equation 𝑥2+𝑦2=25. How many points these two equations have in common?
Now graphically explore the all cases of line and circle intersections in the plane.
(-4,2.99) and (4.8,-1.4)
Now graphically explore the all cases of line and circle intersections in the plane.
(-4,2.99) and (4.8,-1.4)
X+2y = 2 , x²+y² = 25
Y = 1- x/₂
X²+(1-x/₂)² = 25
x²+1-x+x²/₄ = 25
¾ x²-x-24 = 0
x₁ = 4.8 , x₂ = -4.2 y₁ = -1.4 , y₂ = 2.99
(-4,2.99) and (4.8,-1.4)
Y = 1- x/₂
X²+(1-x/₂)² = 25
x²+1-x+x²/₄ = 25
¾ x²-x-24 = 0
x₁ = 4.8 , x₂ = -4.2 y₁ = -1.4 , y₂ = 2.99
(-4,2.99) and (4.8,-1.4)
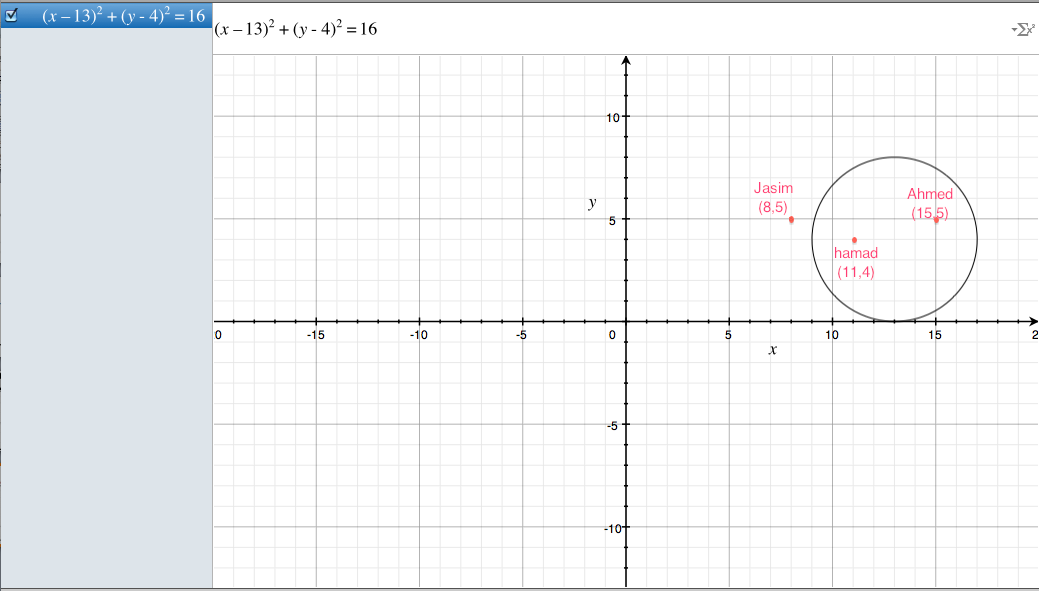
2) THEATER LIGHTING: A bank of lights is arranged over a stage. Each light illuminates a circular area on the stage. A coordinate plane is used to arrange the lights, using the corner of the stage as the origin. The equation (x – 13)2 + (y - 4)2 = 16 represents one of the disks of light. Three actors are located as follows: Hamad is at (11, 4), Jasim is at (8, 5), and Ahmed is at (15, 5). Graph the disk of light to show which actors are in the disk of light?
(Ahmed and hamad in side the disk)
(Ahmed and hamad in side the disk)
3) Space: In order for a satellite to remain in a circular orbit above the Earth, the satellite must be 35,000 km above the Earth. Use the center of the Earth as the origin and 4000 km for the radius of the earth. Write an equation for the orbit of the satellite.
R = 35000+4000 = 39000 km
X²+Y² = (39000)²
X²+Y² = (39000)²
4) Space: Two satellites are orbiting earth. The path of one has the equation. The orbit of the other is 200 km farther from the centre of earth. In one orbit, how much farther does the second satellite travel than the first one?
X²+y² = 2250000
R₁² = 2250000
R₁ = 1500 km
R₂ = 1700 km
C = 2∏r ,
C₁ = 2∏ (1500) = 9425 km
C₂ = 2∏(1700) = 10681 km
C₂-C₁ = 1256 km
X²+y² = 2250000
R₁² = 2250000
R₁ = 1500 km
R₂ = 1700 km
C = 2∏r ,
C₁ = 2∏ (1500) = 9425 km
C₂ = 2∏(1700) = 10681 km
C₂-C₁ = 1256 km
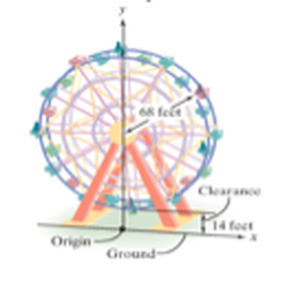
5) The AL-Qasba wheel in the figure has a radius of 68 feet. The clearance between the wheel and the ground is 14 feet. The x-y plane shown has its origin on the ground directly below the center of the wheel. Write the equation of the circular wheel.
Center = (0,82), r = 14
X²+(y-82) ²= 196
Center = (0,82), r = 14
X²+(y-82) ²= 196